drawing 3d from 2d image

Creation of a 3D model from a set of images

This commodity's factual accuracy may be compromised due to out-of-date information. Delight help update this article to reflect recent events or newly available information. (Oct 2019)

A 3D selfie in 1:20 scale printed by Shapeways using gypsum-based printing, created past Madurodam miniature park from second pictures taken at its Fantasitron photo booth.

3D models are generated from 2d pictures taken at the Fantasitron 3D photo booth at Madurodam

Generating and reconstructing 3D shapes from single or multi-view depth maps or silhouettes ^[i]

3D reconstruction from multiple images is the creation of three-dimensional models from a ready of images. It is the reverse process of obtaining 2D images from 3D scenes.

The essence of an image is a projection from a 3D scene onto a 2nd plane, during which process the depth is lost. The 3D point respective to a specific prototype bespeak is constrained to be on the line of sight. From a unmarried prototype, information technology is impossible to decide which betoken on this line corresponds to the paradigm bespeak. If ii images are available, then the position of a 3D point can be found equally the intersection of the two projection rays. This procedure is referred to as triangulation. The key for this process is the relations between multiple views which convey the information that corresponding sets of points must comprise some structure and that this construction is related to the poses and the calibration of the photographic camera.

In recent decades, there is an important need for 3D content for figurer graphics, virtual reality and advice, triggering a change in accent for the requirements. Many existing systems for constructing 3D models are built around specialized hardware (east.thousand. stereo rigs) resulting in a loftier toll, which cannot satisfy the requirement of its new applications. This gap stimulates the use of digital imaging facilities (like a camera). An early on method was proposed by Tomasi and Kanade.^[2] They used an affine factorization approach to extract 3D from images sequences. However, the assumption of orthographic project is a significant limitation of this system.

Processing [edit]

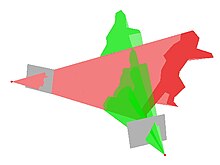
A visual hull can be reconstructed from multiple silhouettes of an object.^[3]

The task of converting multiple second images into 3D model consists of a series of processing steps:

Photographic camera calibration consists of intrinsic and extrinsic parameters, without which at some level no arrangement of algorithms tin can work. The dotted line betwixt Calibration and Depth determination represents that the camera calibration is normally required for determining depth.

Depth determination serves every bit the almost challenging part in the whole process, as information technology calculates the 3D component missing from whatsoever given image – depth. The correspondence problem, finding matches betwixt ii images then the position of the matched elements can then be triangulated in 3D infinite is the primal upshot hither.

Once y'all accept the multiple depth maps yous have to combine them to create a final mesh by calculating depth and projecting out of the camera – registration. Camera calibration will be used to place where the many meshes created past depth maps tin can be combined to develop a larger 1, providing more than one view for ascertainment.

By the stage of Cloth Application you lot accept a complete 3D mesh, which may be the final goal, but ordinarily you will want to apply the colour from the original photographs to the mesh. This tin can range from projecting the images onto the mesh randomly, through approaches of combining the textures for super resolution and finally to segmenting the mesh by cloth, such as specular and diffuse properties.

Mathematical description of reconstruction [edit]

Given a group of 3D points viewed by N cameras with matrices ${\displaystyle \{P^{i}\}_{i=1\ldots N}}$ , ascertain ${\displaystyle m_{j}^{i}\simeq P^{i}w_{j}}$ to be the homogeneous coordinates of the projection of the ${\displaystyle j^{th}}$ point onto the ${\displaystyle i^{th}}$ camera. The reconstruction trouble can be inverse to: given the group of pixel coordinates ${\displaystyle \{m_{j}^{i}\}}$ , find the respective ready of photographic camera matrices ${\displaystyle \{P^{i}\}}$ and the scene construction ${\displaystyle \{w_{j}\}}$ such that

${\displaystyle m_{j}^{i}\simeq P^{i}w_{j}}$ (1)

Generally, without further restrictions, we will obtain a projective reconstruction.^{[4] [5]} If ${\displaystyle \{P^{i}\}}$ and ${\displaystyle \{w_{j}\}}$ satisfy (one), ${\displaystyle \{P^{i}T\}}$ and ${\displaystyle \{T^{-i}w_{j}\}}$ volition satisfy (i) with any 4 × iv nonsingular matrix T.

A projective reconstruction can be calculated by correspondence of points only without whatsoever a priori data.

Machine-calibration [edit]

In auto-calibration or self-calibration, camera motion and parameters are recovered offset, using rigidity. Then construction tin be readily calculated. Two methods implementing this idea are presented equally follows:

Kruppa equations [edit]

With a minimum of three displacements, we can obtain the internal parameters of the photographic camera using a organization of polynomial equations due to Kruppa,^[6] which are derived from a geometric interpretation of the rigidity constraint.^{[vii] [8]}

The matrix ${\displaystyle G=AA^{\peak }}$ is unknown in the Kruppa equations, named Kruppa coefficients matrix. With M and past the method of Cholesky factorization i can obtain the intrinsic parameters easily:

${\displaystyle K={\begin{bmatrix}k_{ane}&k_{2}&k_{3}\\k_{2}&k_{4}&k_{five}\\k_{3}&k_{5}&1\\\cease{bmatrix}}}$

Recently Hartley ^[9] proposed a simpler form. Permit ${\displaystyle F}$ be written as ${\displaystyle F=DUV^{\superlative }}$ , where

Then the Kruppa equations are rewritten (the derivation tin exist found in ^[nine])

Mendonça and Cipolla [edit]

This method is based on the apply of rigidity constraint. Pattern a cost function, which considers the intrinsic parameters as arguments and the fundamental matrices as parameters. ${\displaystyle {F}_{ij}}$ is divers equally the fundamental matrix, ${\displaystyle {A}_{i}}$ and ${\displaystyle {A}_{j}}$ every bit intrinsic parameters matrices.

Stratification [edit]

Recently, new methods based on the concept of stratification have been proposed.^[10] Starting from a projective structure, which tin can be calculated from correspondences only, upgrade this projective reconstruction to a Euclidean reconstruction, past making use of all the available constraints. With this thought the problem can be stratified into different sections: co-ordinate to the corporeality of constraints available, it tin be analyzed at a different level, projective, affine or Euclidean.

The stratification of 3D geometry [edit]

Commonly, the world is perceived as a 3D Euclidean space. In some cases, information technology is not possible to utilise the full Euclidean structure of 3D space. The simplest being projective, so the affine geometry which forms the intermediate layers and finally Euclidean geometry. The concept of stratification is closely related to the serial of transformations on geometric entities: in the projective stratum is a series of projective transformations (a homography), in the affine stratum is a series of affine transformations, and in Euclidean stratum is a series of Euclidean transformations.

Suppose that a fixed scene is captured past two or more perspective cameras and the correspondences between visible points in different images are already given. However, in practice, the matching is an essential and extremely challenging event in computer vision. Here, we suppose that ${\displaystyle n}$ 3D points ${\displaystyle A_{i}}$ are observed by ${\displaystyle m}$ cameras with projection matrices ${\displaystyle P_{j},j=i,\ldots ,m.}$ Neither the positions of point nor the projection of camera are known. Only the projections ${\displaystyle a_{ij}}$ of the ${\displaystyle i^{thursday}}$ point in the ${\displaystyle j^{th}}$ epitome are known.

Projective reconstruction [edit]

Elementary counting indicates we take ${\displaystyle 2nm}$ contained measurements and but ${\displaystyle 11m+3n}$ unknowns, and then the problem is supposed to exist soluble with enough points and images. The equations in homogeneous coordinates can be represented:

${\displaystyle a_{ij}\sim P_{j}A_{i}\qquad i=i,\ldots n,~~j=1,\ldots m}$ (2)

So we tin can utilize a nonsingular four × 4 transformation H to projections ${\displaystyle P_{j}}$ → ${\displaystyle P_{j}H^{-1}}$ and globe points ${\displaystyle A_{i}}$ → ${\displaystyle HA_{i}}$ . Hence, without further constraints, reconstruction is simply an unknown projective deformation of the 3D world.

Affine reconstruction [edit]

See affine space for more than detailed data nearly computing the location of the aeroplane at infinity ${\displaystyle {\Pi }_{\infty }}$ . The simplest way is to exploit prior noesis, for example the information that lines in the scene are parallel or that a point is the ane thirds between 2 others.

We can as well use prior constraints on the photographic camera motility. By analyzing different images of the aforementioned betoken can obtain a line in the direction of motion. The intersection of several lines is the signal at infinity in the motion direction, and one constraint on the affine structure.

Euclidean reconstruction [edit]

By mapping the projective reconstruction to 1 that satisfies a group of redundant Euclidean constraints, nosotros can find a projective transformation H in equation (2).The equations are highly nonlinear and a good initial guess for the construction is required. This can exist obtained by assuming a linear projection - parallel projection, which besides allows piece of cake reconstruction by SVD decomposition.^[2]

Algebraic vs geometric error [edit]

Inevitably, measured data (i.e., epitome or world point positions) is noisy and the noise comes from many sources. To reduce the effect of racket, we usually use more equations than necessary and solve with least squares.

For example, in a typical cypher-space trouble formulation Ax = 0 (like the DLT algorithm), the foursquare of the remainder ||Ax|| is existence minimized with the least squares method.

In general, if ||Ax|| can be considered as a distance between the geometrical entities (points, lines, planes, etc.), then what is existence minimized is a geometric mistake, otherwise (when the error lacks a good geometrical interpretation) it is called an algebraic error.

Therefore, compared with algebraic mistake, we prefer to minimize a geometric fault for the reasons listed:

1. The quantity being minimized has a meaning.
2. The solution is more stable.
3. The solution is abiding under Euclidean transforms.

All the linear algorithms (DLT and others) we have seen so far minimize an algebraic error. Actually, there is no justification in minimizing an algebraic error autonomously from the ease of implementation, as it results in a linear trouble. The minimization of a geometric error is frequently a non-linear problem, that acknowledge only iterative solutions and requires a starting point.

Normally, linear solution based on algebraic residuals serves as a starting point for a not-linear minimization of a geometric cost function, which provides the solution a terminal "polish".^[xi]

Medical applications [edit]

The 2-D imaging has problems of beefcake overlapping with each other and practise non disclose the abnormalities. The 3-D imaging tin exist used for both diagnostic and therapeutic purposes.

iii-D models are used for planning the performance, morphometric studies and has more than reliability in orthopedics.^[12]

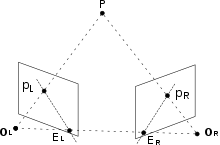
Project of P on both cameras

Problem statement & Basics [edit]

To reconstruct 3-D images from 2-D images taken by a camera at multiple angles. Medical imaging techniques like CT scanning and MRI are expensive, and although CT scans are accurate, they tin induce high radiation doses which is a take chances for patients with certain diseases. Methods based on MRI are not accurate. Since we are exposed to powerful magnetic fields during an MRI scan, this method is not suitable for patients with ferromagnetic metallic implants. Both the methods can exist washed only when in lying position where the global structure of the bone changes. So, we discuss the following methods which tin can exist performed while standing and require low radiation dose.

Though these techniques are iii-D imaging, the region of interest is restricted to a piece; information are acquired to form a fourth dimension sequence.

Stereo Corresponding Point Based Technique [edit]

This method is simple and implemented by identifying the points manually in multi-view radiographs. The first step is to extract the corresponding points in two x-ray images. The second stride is to reconstruct the paradigm in three dimensions using algorithms similar Discrete Linear Transform (DLT).^[13] The reconstruction is only possible where there are Stereo Corresponding Points (SCPs). The quality of the results are dependent on the quantity of SCPs, the more SCPs, the ameliorate the results ^[xiv] but it is deadening and inaccurate. The skill of the operator is a factor in the quality of the image. SCP based techniques are not suitable for bony structures without identifiable edges. More often than not, SCP based techniques are used as function of a process involving other methods.^[15]

Non-Stereo corresponding contour method (NCSS) [edit]

This method uses Ten-ray images for 3D Reconstruction and to develop 3D models with low dose radiations in weight bearing positions.

In NSCC algorithm, the preliminary step is calculation of an initial solution. Firstly anatomical regions from the generic object are defined. Secondly, manual second contours identification on the radiographs is performed. From each radiograph 2D contours are generated using the 3D initial solution object. 3D contours of the initial object surface are projected onto their associated radiograph.^[xv] The 2d association performed between these two set points is based on bespeak-to-point distances and contours derivations developing a correspondence between the 2nd contours and the 3D contours. Next step is optimization of the initial solution. Lastly deformation of the optimized solution is done past applying Kriging algorithm to the optimized solution.^[xvi] Finally, past iterating the final step until the distance betwixt 2 ready points is superior to a given precision value the reconstructed object is obtained.

The advantage of this method is it can be used for bony structures with continuous shape and it too reduced human intervention but they are time-consuming.

Surface rendering technique [edit]

Surface rendering visualizes a 3D object as a fix of surfaces chosen iso-surfaces. Each surface has points with the aforementioned intensity (chosen an iso-value). This technique is usually applied to high contrast data, and helps to illustrate separated structures; for instance, the skull tin can be created from slices of the head, or the blood vessel system from slices of the torso. 2 main methods are:

• Profile based reconstruction: Iso-contours are attached to each other to class iso-surfaces.^[17]
• Voxel based reconstruction: Voxels of the same intensity value are used to form iso-surfaces. Popular algorithms are Marching Cubes, Marching Tetrahedrons and Dividing Cubes.^[17]

Other methods utilise statistical shape models, parametrics, or hybrids of the two

See as well [edit]

• 3D pose estimation – Process of determining spatial characteristics of objects
• 3D reconstruction – Process of capturing the shape and appearance of real objects
• 3D photography
• 2D to 3D conversion – Process of transforming 2D motion-picture show to 3D form
• 3D information acquisition and object reconstruction
• Epipolar geometry – Geometry of stereo vision
• Camera resectioning
• Estimator stereo vision – Extraction of 3D data from digital images
• Structure from motion – Method of 3D reconstruction from moving objects
• Comparison of photogrammetry software
• Visual hull
• Man paradigm synthesis – Computer generation of human images

References [edit]

1. ^ "Soltani, A. A., Huang, H., Wu, J., Kulkarni, T. D., & Tenenbaum, J. B. Synthesizing 3D Shapes via Modeling Multi-View Depth Maps and Silhouettes With Deep Generative Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 1511-1519)". half-dozen March 2020.
2. ^ ^{a b} C. Tomasi and T. Kanade, "Shape and motion from prototype streams under orthography: A factorization approach", International Periodical of Computer Vision, 9(ii):137-154, 1992.
3. ^ A. Laurentini (Feb 1994). "The visual hull concept for silhouette-based image understanding". IEEE Transactions on Pattern Analysis and Machine Intelligence. 16 (two): 150–162. doi:x.1109/34.273735.
4. ^ R. Mohr and Eastward. Arbogast. Information technology tin be washed without photographic camera scale. Pattern Recognition Letters, 12:39-43, 1991.
5. ^ O. Faugeras. What can exist seen in three dimensions with an uncalibrated stereo rig? In Proceedings of the European Briefing on Computer Vision, pages 563-578, Santa Margherita L., 1992.
6. ^ East. Kruppa. Zur Ermittlung eines Objektes aus zwei Perspektiven mit innerer Orientierung. Sitz.-Ber.Akad.Wiss., Wien, math. naturw. Kl., Abt. IIa., 122:1939-1948, 1913.
7. ^ Southward. J. Maybank and O. Faugeras. A theory of self-calibration of a moving photographic camera. International Journal of Reckoner Vision, 8(2):123-151, 1992.
8. ^ O. Faugeras and S. Maybank. Motion from signal matches: multiplicity of solutions. International Journal of Computer Vision, 4(three):225-246, June 1990.
9. ^ ^{a b} R. I. Hartley. Kruppa'southward equations derived from the fundamental matrix. IEEE Transactions on Pattern Assay and Machine Intelligence, 19(2):133-135, February 1997.
10. ^ Pollefeys, Marc. Self-calibration and metric 3D reconstruction from uncalibrated image sequences. Diss. PhD thesis, ESAT-PSI, KU Leuven, 1999.
11. ^ R. Hartley and A. Zisserman. Multiple view geometry in computer vision. Cambridge University Press, 2nd edition, 2003.
12. ^ "Medical Visualization: What is it and what's it for?". GarageFarm. 2018-02-18. Retrieved 2018-02-18 .
13. ^ "Pearcy MJ. 1985. Stereo radiography of lumbar spine move. Acta Orthop Scand Suppl".
14. ^ "Aubin CE, Dansereau J, Parent F, Labelle H, de Guise JA. 1997. Morphometric evaluations of personalised 3D reconstructions and geometric models of the human being spine". Med Biol Eng Comput.
15. ^ ^{a b} "S.Hosseinian, H.Arefi, 3D Reconstruction from multiview medical X-ray images- Review and evaluation of existing methods" (PDF).
16. ^ Laporte, S; Skalli, W; de Guise, JA; Lavaste, F; Mitton, D (2003). "A biplanar reconstruction method based on 2D and 3D contours: application to distal femur". Comput Methods Biomech Biomed Engin. 6 (1): 1–6. doi:10.1080/1025584031000065956. PMID 12623432. S2CID 3206752.
17. ^ ^{a b} G.Scott Owen, HyperVis. ACM SIGGRAPH Education Committee, the National Science Foundation (DUE-9752398), and the Hypermedia and Visualization Laboratory, Georgia State University.

Further reading [edit]

• Yasutaka Furukawa and Carlos Hernández (2015) Multi-View Stereo: A Tutorial [i]
• Flynn, John, et al. "Deepstereo: Learning to predict new views from the globe's imagery." Proceedings of the IEEE Conference on Figurer Vision and Pattern Recognition. 2016.

External links [edit]

• 3D Reconstruction from Multiple Images - discusses methods to excerpt 3D models from plain images.
• Visual 3D Modeling from Images and Videos - a tech-written report describes the theory, practice and tricks on 3D reconstruction from images and videos.
• Synthesizing 3D Shapes via Modeling Multi-View Depth Maps and Silhouettes with Deep Generative Networks - Generate and reconstruct 3D shapes via modeling multi-view depth maps or silhouettes.

allenhicad1961.blogspot.com

Source: https://en.wikipedia.org/wiki/3D_reconstruction_from_multiple_images

Share this post